Krylov-Proportionate Adaptive Filtering
Basic Idea: "Sparsity" or "Sparseness" has been proven a useful property to be exploited in a wide range of research areas including Signal Processing and Coding Theory. One of the most successful examples would be the Low Density Parity Check (LDPC) code. In Audio Adaptive Signal Processing, an innovative paradigm called "Proportionate Adaptive Filtering" has been proposed by Duttweiler in 2000 (see, e.g., Adaptive Filter Theory by S. Haykin). The method works pretty well, provided that the optimal filter (or unknown system) is sparse.
Krylov-Proportionate Adaptive Filtering extends this "Proportionate Adaptive Filtering"
paradigm to
nonsparse (or dispersive) systems.
For this purpose, the paradigm has been changed as follows:
Exploit the sparsity -->
Sparsify the optimal filter
.
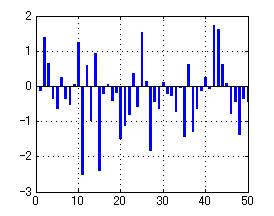 Nonsparse optimal filter
Nonsparse optimal filter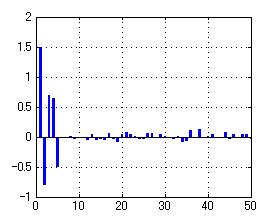 Sparsified optimal filter
Sparsified optimal filter
The algorithm can be seen as a variable-metric projection method.
The variable-metric is defined with positive definite matrices,
which is constructed as
Ωk:=
QΘkQT
with an orthogonal matrix
Q
and
diagonal matrices
Θk
(k stands for time).
Each element of the sparsified optimal filter shown above expresses
the coefficient (of the optimal filter) associated with each column of
Q.
Precisely, the key points are the following:
1. sparsification of the optimal filter based on
Krylov subspace (related to construction of Q),
2. structural constraints on Θk for linear complexity,
3. sparsity extraction (Optimization in the design of Θk).
See [1] for the general idea.
See [2] for the optimization regarding the sparsity extraction.
See [3] for an extension to complex-valued signals and its application to wireless communication systems.
See [4] for an extention to colored input signals (also described in [1]).
See [5], [6] for primitive ideas.
- Masahiro Yukawa, ``Krylov-proportionate adaptive filtering techniques not limited to sparse systems,'' IEEE Trans. Signal Processing, vol.57, no.3, pp.927--943, March 2009.
- Masahiro Yukawa and Wolfgang Utschick, ``Proportionate adaptive algorithm for nonsparse systems based on Krylov subspace and constrained optimization," 34th IEEE ICASSP, pp.3121--3124, Taipei: Taiwan, April 2009.
- Masahiro Yukawa, ``DS/CDMA linear receiver based on Krylov-proportionate adaptive filtering technique ---An extension to complex-valued signals," in Proc. IEEE International Workshop on Machine Learning for Signal Processing, pp.169--174, Cancun: Mexico, October 2008.
- Masahiro Yukawa, ``On whitening for Krylov-proportionate normalized least-mean-square algorithm," in Proc. IEEE International Workshop on Machine Learning for Signal Processing, pp.315--320, Cancun: Mexico, October 2008.
- Masahiro Yukawa, ``Krylov-proportionate NLMS algorithm based on multistage Wiener filter representation,'' in Proc. 33rd IEEE ICASSP, Las Vegas, pp.3801--3804, March--April, 2008.
- Masahiro Yukawa, "An extention of proportionate NLMS algorithm based on multistage Wiener filter representation," in Proc. IEICE SIP Symposium, pp. 526--531, Sendai, November 2007.